Anyone who has worked with a PID controller is familiar with its basic formula:

Based on this formula, you can write an Arduino program that calculates the PID output as shown below:
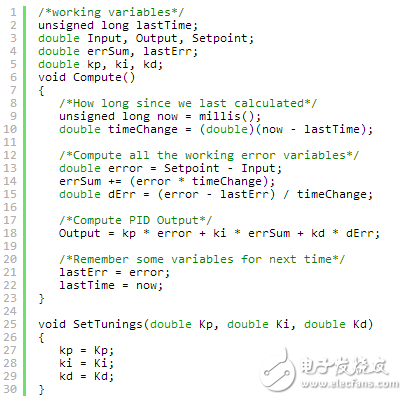
Note: You can copy the source code from the original text.
However, when the PID is called irregularly, two main issues arise:
1. The PID may be called inconsistently, which prevents it from maintaining a stable output.
2. Calculations for the derivative and integral terms require precise time intervals, making them more complex.
To address these problems, ensure that the PID is called at fixed intervals. This allows the controller to perform calculations accurately and consistently. In the revised program, we use a predefined sampling time to trigger the compute function in each cycle. This ensures that the PID can calculate or return the output efficiently.
Here's the updated version of the program:

The gray section represents new additions to the code.
In this improved version, the author converts time to seconds on line 29, simplifying the overall process. Additionally, two new functions are introduced to convert PID parameters into time-based values.
While the PID is running, there may be an issue known as differential overshoot, as illustrated below:
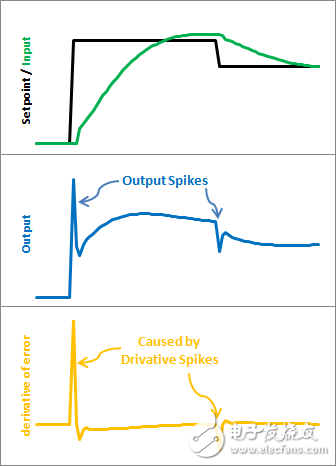
As seen in the diagram, the error is calculated as Setpoint minus Input. Any change in the setpoint causes an abrupt change in the error value. This sudden change in the differential term can lead to instability.
To fix this, we replace the calculation of +dError with -dInput. This adjustment helps prevent overshooting and stabilizes the system.
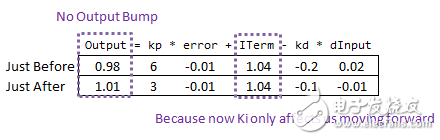
When adjusting PID parameters during runtime, the output can suddenly change, as shown in the following example:
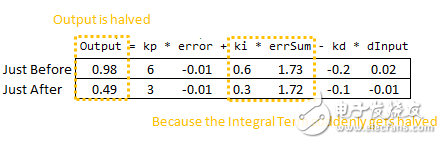
For instance, if we halve the Ki value, the output also halves. This happens because the integral term depends on the accumulated error over time. Changing Ki without resetting the integral sum can cause unexpected behavior.
One solution is to adjust the integral sum (errSum) when changing Ki. For example, if Ki doubles, the integral sum should be halved. This helps maintain stability during parameter changes. Another approach is to store the product of error and Ki, so that future calculations remain consistent even after parameter adjustments.
After implementing this change, the program becomes:
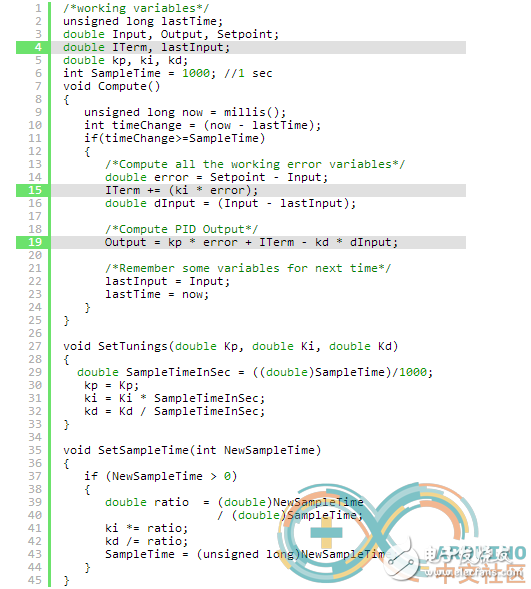
With this modification, the output remains relatively stable even when parameters are adjusted.
This post was last edited by the author on April 13, 2015, at 7:17 PM.
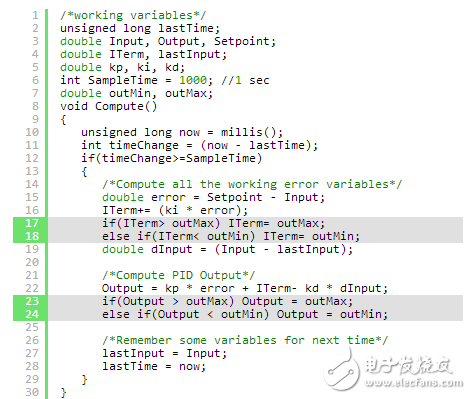
Sometimes, the PID may produce outputs that exceed the physical limits of the system. For example, if the maximum output is 255 but the PID tries to output 300, this can cause issues. To avoid this, we add constraints to the PID output.
Here’s how the program is modified:
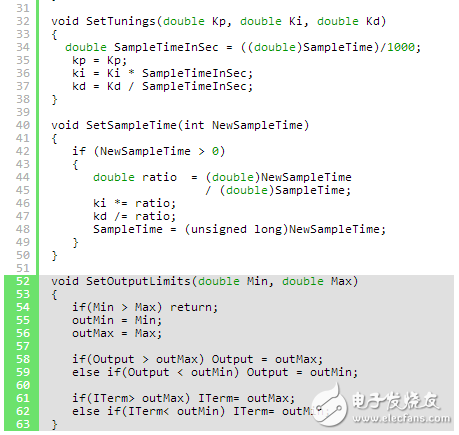
If you want to manually set the output, such as setting it to 0, you might write the loop like this:
void loop()
{
compute();
output = 0;
}
However, this can confuse the PID, as it expects to control the output. When you disable the PID, you should also turn it off to prevent unexpected behavior.
To handle this, we add a switch to enable or disable the PID. When the switch is turned off, the PID does not calculate. When it is turned back on, the PID resumes operation from its last known state.
Here’s the updated program:
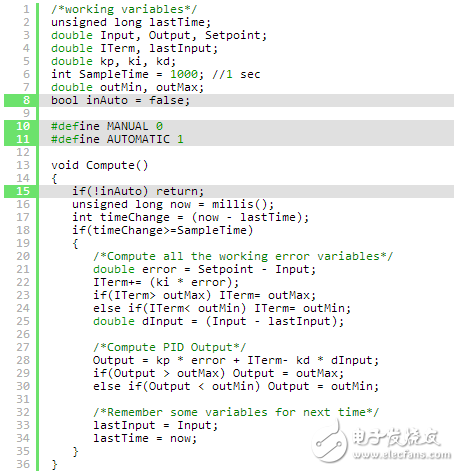
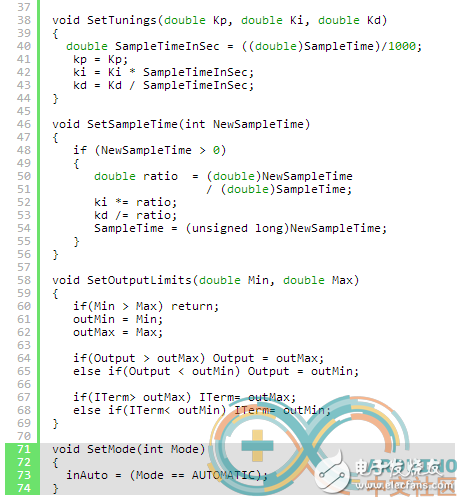
When the switch is re-enabled, the PID output jumps to the last value it sent. To prevent this, we include an initialization function that resets the internal variables. This ensures smooth transitions when the PID is reactivated.
The final program includes the Initialize() function, which updates the last input and integral term to match the current output. This avoids any sudden jumps when the PID starts operating again.
Yixing Guangming Special Ceramics Co.,Ltd , https://www.yxgmtc.com
